4 Tentative de réaction : quelques remarques pratiques

4.1 But du serveur d'exercices

Le but est d'obtenir un certain renouvellement du stock d'exercices de DEUG, dans le sens d'une diversification des activités et des points de vue. Un des avantages de cet objectif est qu'il est suffisamment peu ambitieux pour qu'on puisse immédiatement y travailler concrètement ; ceci est évidemment aussi un de ses défauts. En particulier, il y a certainement bien des choses à repenser dans le contenu mathématique du DEUG ; cependant, réfléchir aux exercices peut éventuellement aider à préparer des changements plus importants ?

Voici quelques principes pratiques concernant plus particulièrement les exercices.

4.2 Faire l'effort d'expliciter les objectifs pédagogiques de chaque feuille d'exercice

En tant qu'enseignant, ceci nous semble indispensable à la fois pour soi-même, pour les collègues qui liront l'exercice, et pourquoi pas pour les étudiants. Ceci permet d'organiser les séances d'exercices selon une certaine progression, de ne pas oublier de traiter certaines notions, d'éviter de présenter plusieurs difficultés nouvelles d'un seul coup, d'évaluer l'enseignement (et pour l'étudiant, de s'auto-évaluer). Ceci devrait permettre aussi de travailler sur le ``à quoi on joue'' (voir la partie 3.6), en explicitant certaines règles du jeu, qui peuvent changer d'un exercice à l'autre. ¹⁵

4.3 Reformuler les exercices

Le contenu mathématique des exercices classiques n'est pas en cause, mais :

- pour y accéder, l'étudiant doit souvent franchir un barrage de formalisme ;

- les énoncés sont souvent présentés sous forme fermée : ``Montrer que...'' ; il faudrait introduire partout un minimum d'incertitude.

Si l'on souhaite vraiment que l'étudiant s'approprie le formalisme, il faut lui proposer des exercices où c'est à lui de formuler de manière précise certaines définitions, certains énoncés. Dans cette optique, voici une reformulation de l'exercice sur les polynômes de Lagrange (voir la partie 2.1) ; cet énoncé était prévu pour un travail en petits groupes, sur une durée importante (plus de deux heures), en présence d'un professeur. Bien sûr, on peut imaginer des formulations intermédiaires entre celle-ci et celle de la partie 2.1.

4.4 L'étudiant doit-il ``avoir appris son cours'' avant le TD ?

Souvent, au début du semestre, on exige des étudiants qu'ils sachent leur cours en arrivant en TD. Quelle que soit la vigueur qu'on mette dans cette exigence, on constate qu'au fil des TD elle est de moins en moins respectée, et on est conduit soit à continuer à faire comme si les étudiants connaissaient leur cours (et on incite ainsi les étudiants à faire semblant de comprendre), soit à réexpliquer rapidement en début de séance les techniques utiles au TD. Dans les deux cas, ceci contribue à répandre parmi les étudiants l'idée que le cours est à la fois incompréhensible et inutile.

Il faudrait sans doute repenser ce rapport entre cours et TD. Pour la plupart des étudiants, digérer l'abstraction d'un cours de maths sans l'aide des TD est impossible ; et l'exigence ci-dessus conduit au mieux (avec beaucoup de bonne volonté) à une mémorisation stérile. Il serait beaucoup plus intéressant d'admettre cette impossibilité, et d'inciter les étudiants à chercher les exercices en lien étroit avec leur cours, en le consultant le plus souvent possible, les exercices aidant à le comprendre. Ce point de vue devrait se ressentir sur les énoncés des exercices. On peut effectivement demander aux étudiants d'avoir une certaine connaissance du cours avant le TD, à condition de se limiter à des objectifs partiels et précis (par exemple en leur fournissant une liste de questions ``simples'', qui leur donne des angles d'attaque) ; on pourrait aussi essayer qu'il y ait une relecture du cours immédiatement après un TD.

4.5 Le problème du temps

Les exercices classiques ont l'avantage de permettre un enseignement relativement rapide d'outils sophistiqués (voir la citation de Guy Brousseau dans la note 10, partie 3.4). Comme toute tentative d'apprentissage plus robuste, les exercices ``alternatifs'' que nous proposons sont souvent beaucoup plus coûteux en temps.

Face à la double contrainte horaires légers/programme chargé, ceci rend difficile le recours fréquent aux exercices non classiques (et peut susciter l'opposition de certains collègues).

Pour contourner ces contraintes en douceur, une possibilité consiste à utiliser les modules optionnels du DEUG (voir par exemple l'expérience du module Culture Mathématique en DEUG MIAS à Orsay). On peut aussi utiliser les ``Devoirs à la Maison''¹⁶.

Bien entendu, il nous semble également souhaitable de diversifier les exercices des TD usuels. On peut espérer que la perte en quantité sera compensée par un gain en qualité ; et la motivation et l'éclairage apportés par les exercices ``alternatifs'' peuvent rendre plus efficaces les activités plus techniques.

4.6 Résistances

Si l'on veut vraiment faire passer cette diversification dans les m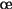urs (des enseignants et des étudiants), il faudra sans doute atteindre une certaine masse critique : si on se contente de proposer un exercice différent de temps en temps, il sera juste ressenti comme un exercice bizarre : ``d'ailleurs, il n'y en a pas dans les annales d'examens''... Ce qui nous amène à une deuxième condition : tout changement de pratique, pour être adopté, doit avoir une répercussion d'une manière ou d'une autre sur l'examen¹⁷. Il faudrait donc introduire explicitement des questions plus ouvertes dans les énoncés, ce qui nécessite des épreuves plus longues (en temps, pas en quantité d'exercices). Au passage, cela pourrait contribuer à diminuer l'importance excessive donnée à la rapidité : notre but n'est pas de former les étudiants à passer des concours, et l'université devrait pouvoir affirmer le droit à une certaine lenteur.

Notes

... l'autre.¹⁵

À un niveau plus global, il est ahurissant de constater que les objectifs des modules d'enseignement sont très rarement explicités, et jamais expliqués aux enseignants débutants. Par exemple, le rôle des enseignements utilisant des logiciels de calculs formels n'est pas éclairci : s'agit-il d'apprendre à maîtriser le logiciel, ou juste de l'utiliser pour faire les calculs dans les exercices classiques, ou de l'utiliser pour faire des maths expérimentales ?

... Maison''¹⁶

Les DMs sont souvent massivement boycottés par les étudiants ; il ne serait donc pas ridicule d'essayer de les rendre plus motivants.

... l'examen¹⁷

Pour éviter les gros couacs, on peut envisager d'``expérimenter'' sur les épreuves moins importantes : tests, interros...